Diện tích hình trụ: Diện tích xung quanh hình trụ, diện tích toàn phần hình trụ

Cùng mò mẫm hiểu về công thức tính diện tích S xung xung quanh, diện tích S toàn phần và độ cao của hình trụ nhằm vận dụng vô học hành và cuộc sống từng ngày nhé.

Cách tính diện tích S hình trụ

Diện tích hình trụ bao gồm sở hữu diện tích S xung xung quanh và diện tích S toàn phần.

Các chúng ta có thể nhập độ dài rộng độ cao, nửa đường kính của hình trụ vô bảng sau đây biết diện tích S xung xung quanh và diện tích S toàn phần của hình trụ.

Công thức tính diện tích S xung xung quanh hình trụ

Diện tích xung xung quanh hình trụ chỉ bao hàm diện tích S mặt mày xung xung quanh, xung quanh hình trụ, ko bao gồm diện tích S nhị lòng.

Công thức tính diện tích S xung xung quanh hình trụ bởi vì chu vi lối tròn trặn lòng nhân với độ cao.

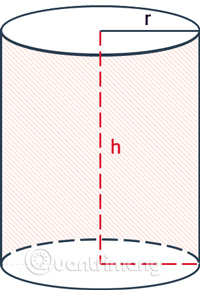Trong đó:

S_{xung xung quanh}là diện tích S xung xung quanh.
r là nửa đường kính hình trụ.
h là độ cao, khoảng cách thân mật 2 lòng của hình trụ.

Ví dụ: 1

Một hình trụ tròn trặn sở hữu nửa đường kính lòng r = 5 centimet, độ cao h = 7cm. Tính diện tích S xung xung quanh hình trụ đứng.

Giải: Diện tích xung xung quanh của hình trụ tròn: Sxq = 2.π.r.h = 2π.5.7 = 70π = 219,8 (cm²).

Ví dụ: 2

Cho hình vuông vắn ABCD cạnh 2a. Gọi O và O’ thứu tự là trung điểm những cạnh AB và CD. Khi tảo hình vuông vắn cơ xung xung quanh trục OO’ tớ được một hình trụ tròn trặn xoay. Tính diện tích S xung xung quanh hình trụ tròn trặn xoay cơ.

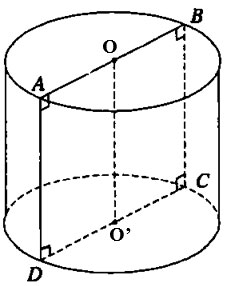
Tính diện tích S hình trụ

Lời giải:

Bán kính lối tròn trặn lòng là r= CD= a

Chiều cao hình trụ là h= OO'= AD=2a

Vậy diện tích S xung xung quanh hình trụ là Sxq = 2πrh = 2π.a.2a =4a2π

Công thức tính diện tích S toàn phần hình trụ

Diện tích toàn phần được xem là kích cỡ của toàn cỗ không khí hình rung rinh lưu giữ, bao hàm cả diện tích S xung xung quanh và diện tích S nhị lòng tròn trặn.

Công thức tính diện tích S toàn phần hình trụ bởi vì diện tích S xung xung quanh cùng theo với diện tích S của 2 lòng.

Ví dụ 1: Tính diện tích S toàn phần của hình trụ sở hữu lòng bởi vì 3 và độ cao bởi vì 5.

Lời giải:

Diện tích toàn phần là Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π

Tính độ cao hình trụ

Chiều cao hình trụ đó là khoảng cách thân mật nhị mặt mày lòng của hình trụ.

Tính độ cao hình trụ lúc biết diện tích S toàn phần và nửa đường kính đáy

$h=\frac{\text { Stoan phan }-2 \pi r^2}{2 \pi r}$

Ví dụ: Cho hình trụ sở hữu nửa đường kính lòng R = 8cm và diện tích S toàn phần 564π cm2 . Tính độ cao của hình trụ.

Giải:

Ta sở hữu $h=\frac{564 \pi-2 \pi 8^2}{2 \pi 8}=\frac{564 \pi-128 \pi}{16 \pi}$ $=\frac{436 \pi}{16 \pi}=27,25 \mathrm{~cm}$

Tính độ cao hình trụ lúc biết diện tích S xung quanh

=> $h=\frac{Sxq}{2\pi r}$

Công thức tính nửa đường kính lòng của hình trụ

1. Công thức tính chu vi lối tròn; diện tích S hình tròn

Đường tròn trặn sở hữu chu vi C=2πr

=> $r=\frac{C}{2 \pi}$

Hình tròn trặn lòng sở hữu diện tích S S=πr²

=> $r=\sqrt{\frac{S}{\pi}}$

Ví dụ. Tính nửa đường kính lòng của hình trụ trong số tình huống sau:

a. Chu vi lối tròn trặn lòng là 6π

b. Diện tích lòng là 25π

Lời giải:

a. Bán kính lối tròn trặn lòng là

$r=\frac{C}{2 \pi}=\frac{6 \pi}{2 \pi}=3$

b. Bán kính lối tròn trặn lòng là

$\mathrm{r}=\sqrt{\frac{\mathrm{S}}{\pi}}=\sqrt{\frac{25 \pi}{\pi}}=5$

2. Đáy là lối tròn trặn nội tiếp nhiều giác

- Nội tiếp tam giác bất kì: $\mathrm{R}=\frac{\mathrm{S}}{\mathrm{p}}$ với S là diện tích S tam giác và p là nửa chu vi

- Nội tiếp tam giác đều: $R=\frac{\sqrt{3}}{6}$ cạnh

- Nội tiếp hình vuông: $\mathrm{R}=\frac{\text { cạnh }}{2}$

Ví dụ 1. Cho hình trụ nội tiếp vô một hình lập phương sở hữu cạnh a. Tính nửa đường kính của hình trụ cơ.

Bán kính hình trụ là: $R=\frac{a}{2}$

Ví dụ 2. Cho lăng trụ đều ABC.A’B’C’ sở hữu , thể tích nước ngoài tiếp khối trụ. Tính nửa đường kính khối trụ cơ.

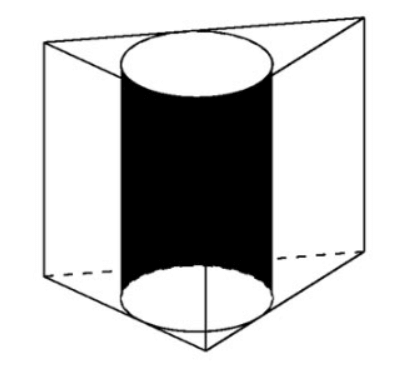
Hình trụ

Thể tích khối lăng trụ là $\mathrm{V}=\mathrm{h} \cdot \mathrm{S}_{\mathrm{d}} \Leftrightarrow=\frac{\mathrm{a}^3 \sqrt{3}}{2}$ $=\mathrm{a} \cdot \mathrm{S}_{\mathrm{d}} \Rightarrow>\mathrm{S}_{\mathrm{d}}=\frac{\mathrm{a}^2 \sqrt{3}}{2}$

Đáy lăng trụ đều là tam giác đều nên $\mathrm{S}_{\mathrm{d}}=\operatorname{cạnh}^2 \frac{\sqrt{3}}{4}$ => cạnh $=\mathrm{a} \sqrt{2}$

Do vậy nửa đường kính lòng hình trụ là: $\mathrm{R}=\frac{\mathrm{a} \sqrt{2} \cdot \sqrt{3}}{6}=\frac{\mathrm{a}}{\sqrt{6}}$

3. Đáy là lối tròn trặn nước ngoài tiếp nhiều giác

Ngoại tiếp tam giác bất kì: $\mathrm{R}=\frac{\mathrm{abc}}{4 \mathrm{~S}}=\frac{\mathrm{abc}}{4 \sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}}$

Trong đó:

a, b, c là phỏng lâu năm 3 cạnh tam giác
p là nửa chu vi tam giác: $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$

Ngoại tiếp tam giác vuông: $\mathrm{R}=\frac{1}{2}$ cạnh huyền

Ngoại tiếp tam giác đều: $R=\frac{\sqrt{3}}{3}$ cạnh

Ngoại tiếp hinh vuông: $R=\frac{\sqrt{2}}{2}$ cạnh

Ví dụ:

Tính nửa đường kính lòng của khối trụ nước ngoài tiếp khối chóp đều S.ABC trong số tình huống sau:

a. ABC là tam giác vuông bên trên A sở hữu AB = a và AC = a√3

b. ABC sở hữu AB= 5; AC= 7; BC=8

Giải:

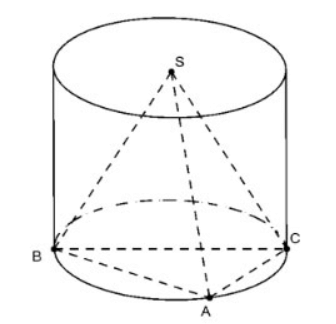
Khối trụ nước ngoài tiếp khối chóp đều

a. Cạnh huyền $\mathrm{BC}=\sqrt{\mathrm{AB}^2+\mathrm{AC}^2}$ $=\sqrt{\mathrm{a}^2+3 \mathrm{a}^2}=2 \mathrm{a}$

Do ABC vuông bên trên A nên nửa đường kính R=0,5.BC=a

b. Nửa chu vi tam giác ABC là ${p}=\frac{5+7+8}{2}=10$
$\Rightarrow \mathrm{S}=\sqrt{10 .(10-5)(10-7)(10-8)}=10 \sqrt{3}$
$\Rightarrow \mathrm{R}=\frac{\mathrm{abc}}{4 \mathrm{~S}}=\frac{5.7 .8}{40 \sqrt{3}}=\frac{7 \sqrt{3}}{3}$

Hình trụ tròn trặn là gì

Hình trụ tròn là hình trụ sở hữu 2 lòng là hình trụ đều nhau và tuy vậy song cùng nhau.

Hình trụ được dùng khá phổ cập trong số Việc hình học tập kể từ căn bạn dạng cho tới phức tạp, vô cơ công thức tính diện tích S, thể tích hình trụ thông thường được dùng không giống phổ cập. Nếu chúng ta đã biết phương pháp tính diện tích S và chu vi hình trụ thì cũng rất có thể đơn giản tư duy rời khỏi những công thức tính thể tích, diện tích S xung xung quanh tương tự diện tích S toàn phần của hình trụ.

Công thức tính diện tích S tiết diện của hình trụ

Cắt hình trụ bởi vì mặt mày phẳng lặng (P) qua loa trục

Thiết diện sẽ có được là một trong hình chữ nhật.

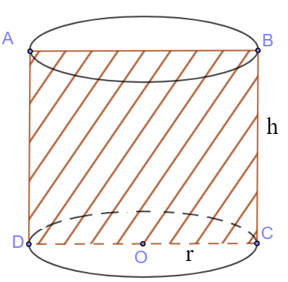Diện tích thiết diện:

SABCD = BC.CD =2r.h

Cắt hình trụ bởi vì mặt mày phẳng lặng (P) tuy vậy song và cơ hội trục một khoảng chừng x

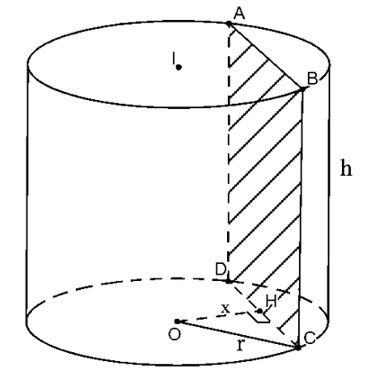Thiết diện tạo nên trở nên là hình chữ nhật ABCD như hình bên trên.

Gọi H là trung điểm CD tớ sở hữu OH ⊥ CD=>

$CD=2\sqrt{r^2-x^2}$

Do cơ diện tích S thiết diện

$S_{ABCD}=CD.BC=2h\sqrt{r^2-x^2}$

Cắt hình trụ bởi vì mặt mày phẳng lặng (P) ko vuông góc với trục tuy nhiên tách toàn bộ những lối sinh của hình trụ

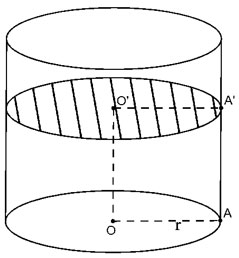Thiết diện tạo nên trở nên là hình trụ tâm O’ nửa đường kính O'A'=r

Diện tích thiết diện: S= πr2

Cắt hình trụ bởi vì mặt mày phẳng lặng (P) ko vuông góc với trục tuy nhiên tách toàn bộ những lối sinh của hình trụ.

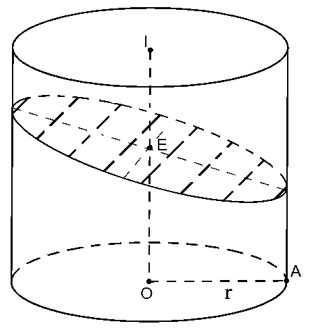Thiết diện tạo nên trở nên là Elip (E) sở hữu trục nhỏ 2r => a=r

Trục rộng lớn bởi vì

với là góc thân mật trục OI với (P)

Do cơ diện tích S S= π. a.b=

Ví dụ tính diện tích S hình trụ

Bài 1:

Diện tích xung xung quanh của một hình trụ sở hữu chu vi hình trụ lòng là 13cm và độ cao là 3cm.

Giải:

Ta có: chu vi hình trụ C = 2R.π = 13cm, h = 3cm

Vậy diện tích S xung xung quanh của hình trụ là :

Sxq = 2πr.h = C.h = 13.3 = 39 (cm²)

Bài 2: Cho một hình trụ sở hữu nửa đường kính lối tròn trặn lòng là 6cm, trong lúc cơ độ cao nối kể từ lòng cho tới đỉnh hình trụ dày 8 centimet. Hỏi diện tích S xung xung quanh và diện tích S toàn phần của hình trụ bởi vì bao nhiêu?

Giải

Theo công thức tớ sở hữu chào bán lối tròn trặn lòng r = 6 centimet và độ cao của hình trụ h = 8 centimet . Suy rời khỏi tớ sở hữu công thức tính diện tích S xung xung quanh hình trụ và diện tích S toàn phần hình trụ bằng:

Diện tích xung xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm²

Diện tích toàn phần hình trụ = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²

Bài 3: Một hình trụ sở hữu nửa đường kính lòng là 7cm, diện tích S xung xung quanh bởi vì 352cm2.

Khi cơ, độ cao của hình trụ là:

(A) 3,2 cm; (B) 4,6cm; (C) 1,8 cm

(D) 2,1cm; (E) Một thành phẩm khác

Hãy lựa chọn thành phẩm trúng.

Giải: Ta có

$Sxq=2\pi rh\ =>\ h=\frac{Sxq}{2\pi r}=\ \frac{352}{2\pi7}=8$

Vậy, đáp án E là đúng mực.

Bài 4: Chiều cao của một hình trụ bởi vì nửa đường kính lối tròn trặn lòng. Diện tích xung xung quanh của hình trụ 314 cm2. Hãy tính nửa đường kính lối tròn trặn lòng và thể tích hình trụ (làm tròn trặn thành phẩm cho tới chữ số thập phân loại hai).

Công thức tính thể tích hình trụ

Giải:

Diện tích xung xung quanh hình trụ bởi vì 314cm2

Ta sở hữu Sxq = 2.π.r.h = 314

Mà r = h

Nên 2πr² = 314 => r² ≈ 50 => r ≈ 7,07 (cm)

Thể tích hình trụ: V = π.r2.h = π.r3 ≈ 1109,65 (cm³).

Hy vọng nội dung bài viết bên trên đang được khiến cho bạn cầm được những kiến thức và kỹ năng cơ bạn dạng tương tự nâng lên về hình trụ, phương pháp tính diện tích S toàn phần và diện tích S xung xung quanh của hình trụ.