Câu hỏi:
25/10/2024 5,879
A. 5 mặt mày, 5 cạnh
B. 6 mặt mày, 5 cạnh
C. 6 mặt mày, 10 cạnh
Đáp án chủ yếu xác
D. 5 mặt mày, 10 cạnh
Đáp án đúng: C
*Phương pháp giải:
- Nắm vững vàng lại kỹ năng về hình chóp đều: khái niệm, số mặt mày, số đỉnh, số cạnh,.....
*Lời giải:
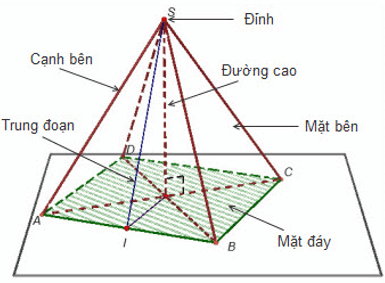
Hình chóp ngũ giác với 5 mặt mày mặt +1 mặt mày lòng. 5 cạnh mặt mày và 5 cạnh lòng.
*Lý thuyết tăng về hình chóp tứ giác đều
Hình chóp đều là hình chóp có đáy là một nhiều giác đều, các mặt mặt mày là những tam giác cân nặng bằng nhau có công cộng đỉnh.
+ Chân đường cao của hình chóp đều trùng với tâm của đường tròn trải qua các đỉnh của mặt đáy.
+ Đường cao vẽ từ đỉnh của mỗi mặt mặt mày của hình chóp đều được gọi là trung đoạn của hình chóp đó.
a) Diện tích xung xung quanh của hình chop đều
Diện tích xung xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn:
Sxq = p.d (p: nửa chu vi đáy, d: trung đoạn)
b) Diện tích toàn phần của hình chóp
Diện tích toàn phần của hình chóp bằng tổng của không gian xung xung quanh và không gian đáy:
Stp = Sxq + S (S: không gian đáy)
c) Thể tích của hình chóp bằng một phần phụ vương của không gian đáy nhân với chiều cao:
V = 1/3S.h (S: không gian đáy, h: chiều cao)
Xem tăng những tìm hiểu thêm hoặc, chi tiết:
Trắc nghiệm Hình chóp đều và hình chóp cụt đều (có đáp án)
Trắc nghiệm Thể tích hình chóp đều (có đáp án)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt mày phẳng lặng mang đến tứ giác ABCD, điểm . Hỏi với từng nào mặt mày phẳng lặng phân biệt tạo nên vì thế phụ vương vô năm điểm A,B,C,D,E?
Câu 2:
Cho tứ giác ABCD. cũng có thể xác lập được từng nào mặt mày phẳng lặng chứa chấp toàn bộ những đỉnh của tứ giác ABCD.
Câu 3:
Cho tứ giác lồi ABCD và điểm S ko nằm trong mp(ABCD). Có từng nào mặt mày phẳng lặng phân biệt xác lập vì thế 3 vô số những điểm A,B,C,D,S?
Câu 4:
Trong , mang đến tứ điểm A,B,C,D vô cơ không tồn tại phụ vương điểm này trực tiếp sản phẩm. Điểm . Có bao nhiêu mặt mày phẳng lặng tạo nên vì thế S và nhị vô số tứ điểm trình bày trên?
Câu 5:
Trong những xác minh sau, xác minh này đúng?
Câu 6:
Trong những mệnh đề sau mệnh đề này sai?
Câu 7:
Trong những hình sau:
Các hình rất có thể là hình trình diễn của một hình tứ diện là:
Câu 8:
Các nhân tố này tại đây xác lập một phía phẳng lặng duy nhất?
Câu 9:
Cho năm điểm A,B,C,D,E vô cơ không tồn tại tứ điểm này phía trên và một mặt mày phẳng lặng. Hỏi với từng nào mặt mày phẳng lặng tạo nên vì thế phụ vương vô số thời gian điểm đang được cho?
Câu 10:
Cho 2 đường thẳng liền mạch a, b cắt nhau và ko trải qua điểm A. Xác quyết định được không ít nhất từng nào mặt mày phẳng lặng vì thế a, b và A?
Câu 11:
Cho tứ điểm ko đồng phẳng lặng, tớ rất có thể xác lập được không ít nhất từng nào mặt mày phẳng lặng phân biệt kể từ tứ điểm đang được cho?
Câu 12:
Hình này tại đây vẽ đích quy tắc?
Câu 13:
Số thành phần của tụ họp những điểm công cộng của một đường thẳng liền mạch và một phía phẳng lặng ko thể là:
Câu 14:
Một hình không khí với hình chiếu đứng (nhìn từ xưa vô (có thể nom kể từ sau) nhằm kể từ hình 3 chiều gửi lịch sự hình 2D) hình chiếu vì thế (nhìn kể từ bên trên xuống) rất có thể nom kể từ bên dưới lên)), hình chiếu cạnh (từ trái ngược lịch sự (có thể nom kể từ nên sang)) theo lần lượt được thể hiện nay như sau:
Hãy vẽ hình trình diễn của hình đó?