I. Lý thuyết
1. Khái niệm
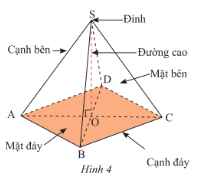
Hình chóp tứ giác đều có:
- Đáy là hình vuông vắn.
- 4 cạnh mặt mũi đều bằng nhau.
- 4 mặt mũi mặt là những tam giác thăng bằng nhau và sở hữu công cộng một đỉnh.
- 4 cạnh lòng đều bằng nhau là tư cạnh của hình vuông vắn lòng.
- Chân lối cao trùng với uỷ thác điểm của hai tuyến phố chéo cánh của mặt mũi lòng.
2. Công thức tính diện tích S xung xung quanh của hình chóp tứ giác đều
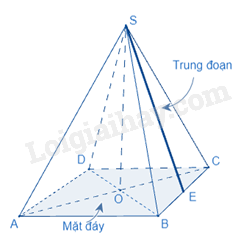
Diện tích xung xung quanh của hình chóp tam giác đều vì chưng nửa chu vi lòng với phỏng nhiều năm trung đoạn.
\(S_{xq}=p.d\)
(\(S_{xq}\) là diện tích S xung xung quanh, p là nửa chu vi lòng, d là trung đoạn)
3. Công thức tính thể tích của hình chóp tứ giác đều
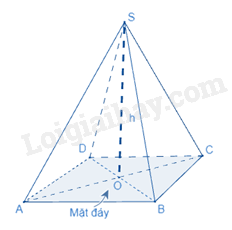
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) vì chưng \(\frac{1}{3}\) diện tích S lòng nhân với độ cao.
\(V = \frac{1}{3}{S_{đáy}}.h\)
(V là thể tích, \({S_{đáy}}\) là diện tích S lòng, h là chiều cao)
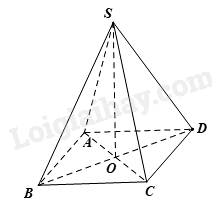
Ví dụ:
Cho hình chóp tứ giác đều sau:

Thể tích của hình chóp là: \(V = \frac{1}{3}.6.16.16 = 512(c{m^3})\)
II. Bài tập luyện vận dụng
Câu 1. Trong những tấm bìa bên dưới, sở hữu bao nhiêu hình vội vàng lại được trở nên hình chóp tứ giác đều
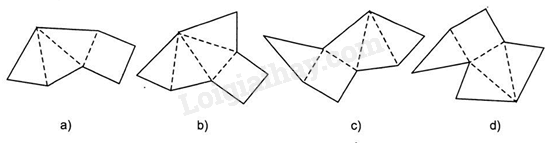
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải
Hình a khi vội vàng lại thì không được một hình chóp đều vì như thế lòng là tứ giác đều tuy nhiên chỉ mất tía mặt mũi mặt thay cho nên sở hữu 4 mặt mũi mặt mũi.
Hình b, c khi vội vàng lại thì được một hình chóp tứ giác đều.
Hình d khi vội vàng lại thì không được một hình chóp tứ giác đều vì như thế phía trên và một cạnh lòng sở hữu cho tới 2 mặt mũi mặt còn bên trên một cạnh lòng thì ko xuất hiện mặt mũi này.
Đáp án: B
Câu 2. Cho hình chóp tứ giác đều sở hữu toàn bộ những cạnh đều bằng nhau, nếu như tăng cạnh mặt mũi lên nhị chuyến thì chu vi mặt mũi lòng sẽ:
A. Giảm chuồn 2 lần
B. Tăng lên 2 lần
C. Giảm chuồn 4 chuyến.
D. Tăng lên 4 chuyến.
Lời giải
Hình chóp tứ giác đều phải có lòng là hình vuông vắn, toàn bộ những cạnh đều đều bằng nhau nên cạnh mặt mũi tạo thêm nhị chuyến thì cạnh lòng tăng nhị chuyến. Khi cơ chu vi hình vuông vắn cũng tạo thêm gấp đôi.
Đáp án: B
Câu 3. Chọn câu vấn đáp đúng: Hình chóp tứ giác đều có:
A. 4 cạnh, 1 đỉnh, 4 mặt
B. 8 cạnh, 1 đỉnh, 5 mặt
C. 6 cạnh, 1 đỉnh, 4 mặt
D. 8 cạnh, 4 đỉnh, 5 mặt
Lời giải
Hình chóp tứ giác đều có một đỉnh, 8 cạnh và 5 mặt mũi.
Đáp án: B
Câu 4. Tính diện tích S xung xung quanh của hình chóp tứ giác đều biết độ cao một phía mặt mũi của hình chóp vì chưng 5cm, cạnh lòng của hình chóp vì chưng 4cm.
A. \(20c{m^2}\).
B. \(60c{m^2}\).
C. \(40c{m^2}\)
D. \(80c{m^2}\)
Lời giải
Diện tích xung xung quanh của hình chóp tứ giác đều vì chưng tổng diện tích S những mặt mũi mặt tuy nhiên hình chóp tứ giác đều sở hữu 4 mặt mũi mặt nên \({S_{xq}} = S.4 = (\frac{1}{2}.5.4).4 = 40c{m^2}\) nên lựa chọn đáp án C.
Đáp án: C
Câu 5. Cho hình chóp tứ giác đều sở hữu cạnh lòng vì chưng 4cm, độ cao của hình chóp là \(9cm\). Tính thể tích của hình chóp cơ.
Lời giải
Theo công thức thể tích của hình chóp tam giác đều: \(V = \frac{1}{3}.S.h = \frac{1}{3}.(4.4).9 = 48c{m^3}\)
Câu 6. Cho khối chóp tứ giác đều, nếu như tăng cạnh lòng lên tía chuyến và hạn chế độ cao chuồn tía chuyến thì thể tích của khối chóp sẽ:
A. Giảm chuồn 9 chuyến.
B. Tăng lên 3 chuyến.
C. Giảm chuồn 3 chuyến.
D. Tăng lên 9 chuyến.
Lời giải
Nếu cạnh lòng tạo thêm 3 chuyến thì diện tích S lòng tăng 9 chuyến. Vì độ cao sụt giảm 3 chuyến nên thể tích khối chóp tạo thêm 3 chuyến.
Đáp án: B
Câu 7. Một hình chóp tứ giác đều hoàn toàn có thể tích vì chưng \(50c{m^3}\), độ cao hình chóp vì chưng 6cm, độ cao mặt mũi mặt vì chưng 4cm. Tính diện tích S xung xung quanh hình chóp cơ.
Lời giải
Diện tích lòng của hình chóp là : \(50.3:6 = 25c{m^2}\)
Gọi x là phỏng nhiều năm cạnh lòng, vì như thế lòng hình chóp tứ giác đều là hình vuông vắn nên tớ có
\({x^2} = 25 \Rightarrow x = 5cm\).
Diện tích một phía mặt mũi là: \(S = \frac{1}{2}.5.4 = 10(c{m^2})\)
Diện tích xung xung quanh của hình chóp bên trên là: \({S_{xq}} = 4.S = 4.10 = 40(c{m^2})\)
Câu 8. Cho hình chóp tứ giác đều S. ABCD sở hữu diện tích S xung xung quanh vì chưng \(72c{m^2}\) , độ cao có tính nhiều năm vì chưng 6cm, độ cao một phía mặt mũi là 4cm .Thể tích của khối chóp cơ là?
Lời giải
Diện tích một phía mặt mũi là: \(72:4 = 18c{m^2}\)
Độ nhiều năm cạnh lòng là: \(18.2:4 = 9cm\)
Diện tích mặt mũi lòng là: \({S_{ABCD}} = 9.9 = 81c{m^2}\)
Áp dụng công thức thể tích khối chóp tớ được: \(V = \frac{1}{3}.81.6 = 162c{m^3}\)
Câu 9. Một cái bể hình vỏ hộp chữ nhật đựng nước, sở hữu chiều nhiều năm 1,2m; chiều rộng lớn 0,9m, độ cao 1m. Hiện bên trên mực nước nhập bể cao 0,5m. Người tớ sử dụng 1 cái gầu hình chóp tam giác đều diện tích S lòng \(1800c{m^2}\), độ cao 20cm nhằm múc nước nhập bể. Cần múc từng nào chuyến nhằm lênh láng nước nhập bể? (mỗi chuyến múc lênh láng gầu)
Lời giải
Thể tích nước cần thiết nhằm ụp nhập bể là:
\({V_{nuoc}} = 1,2.0,9.(1 - 0,5) = 0,54({m^3}) = 540\)(lít)
Thể tích gầu nước là:
\({V_{gau}} = \frac{1}{3}.1800.trăng tròn = 12000(c{m^3}) = 12\)(lít)
Số chuyến cần thiết múc nhằm không còn nước nhập bể là: \(540:12 = 45\)(lần)
Câu 10. Người tớ thực hiện một bugalow dạng hình chóp tứ giác đều sở hữu độ cao 4m, cạnh sàn ngôi nhà vì chưng 6m. Người tớ phân chia song thực hiện nhị tầng vì chưng một phía phẳng lì tuy nhiên song với sàn, cơ hội đỉnh của hình chóp một khoảng chừng vì chưng nửa độ cao, cạnh sàn nhà tầng nhị vì chưng 1/2 cạnh sàn nhà tầng một. lõi một người cần thiết \(3{m^3}\)không khí, tính số người tối nhiều trên tầng bên dưới. ( hình vẽ dưới)
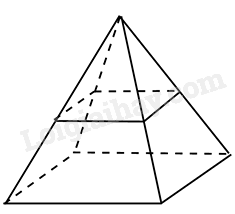
Lời giải
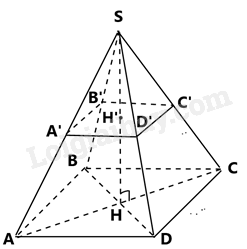
\(SH = 4m\)là độ cao của bugalow
\( \Rightarrow SH' = \frac{{SH}}{2} = 2m\)
\(A'B' = \frac{1}{2}.AB = \frac{1}{2}.6 = 3m\)
Ta có:
\(\begin{array}{l}{S_{A'B'C'D'}} = 3.3 = 9{m^2}\\{S_{ABCD}} = 6.6 = 36{m^2}\end{array}\)
\(\begin{array}{l}{V_{S.A'B'C'D'}} = \frac{1}{3}.{S_{A'B'C'D'}}.SH' = \frac{1}{3}.9.2 = 6{m^3}\\{V_{S.ABCD}} = \frac{1}{3}.{S_{ABCD}}.SH = \frac{1}{3}.36.4 = 48{m^3}\end{array}\)
Thể tích phần không khí sót lại trên tầng bên dưới là: \(V = {V_{S.ABCD}} - {V_{S.A'B'C'D'}} = 48 - 6 = 42{m^3}\)
