Hình chóp đều là gì? Hình chóp đều tam giác, hình chóp đều tứ giác

Hình chóp đều

Hình chóp đều: Hình chóp đều tam giác, hình chóp đều tứ giác hỗ trợ những khái niệm, đặc thù hình chóp tam giác đều, phân biệt hình chóp tam giác đều và hình chóp tứ giác đều, phương pháp vẽ hình chóp tam giác đều, công thức tính thể tích hình chóp tam giác đều.. hùn những em nắm rõ kỹ năng và kiến thức được học tập, áp dụng thực hiện bài xích tập luyện dễ dàng và đơn giản rộng lớn.

1. Hình chóp đều (Hình chóp nhiều giác đều) là gì?

- Hình chóp đều (hình chóp nhiều giác đều) là hình chóp đem lòng là nhiều giác đều và hình chiếu của đỉnh xuống lòng trùng với tâm của lòng ... Hình chóp đều là hình chóp đem lòng là nhiều giác đều; những cạnh mặt mũi đều nhau.

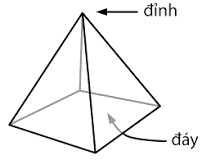
Hình chóp đều là gì? Hình chóp đều tam giác, hình chóp đều tứ giác

a. Tính chất: Chân lối cao của hình chóp nhiều giác đều là tâm của lòng.

b. Thể tích hình chóp đều: $V = \frac{1}{3}.S.h$ $V = \frac{1}{3}.S.h$

Trong đó: S là diện tích S lòng, h là chiều cao

c. Thể tích hình chóp cụt đều: $V = \frac{1}{3}.h.\left( {B.B$ $V = \frac{1}{3}.h.\left( {B.B' + \sqrt {B.B'} } \right)$

Trong đó:

B và B’ theo lần lượt là diện tích S của lòng rộng lớn và lòng nhỏ của hình chóp cụt đều.

h là độ cao (khoảng cơ hội thân thích 2 mặt mũi đáy).

2. Hình chóp tam giác đều

- Hình chóp tam giác đều là hình chóp đem lòng là tam giác đều, những mặt mũi mặt (cạnh bên) đều đều nhau hoặc hình chiếu của đỉnh chóp xuống lòng trùng với tâm của tam giác đều.

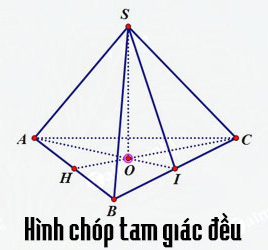
Hình chóp đều: Hình chóp đều tam giác, hình chóp đều tứ giác

a. Tính hóa học hình chóp tam giác đều

Đáy là tam giác đều
Tất cả những cạnh mặt mũi vì thế nhau
Tất cả những mặt mũi mặt là những tam giác thăng bằng nhau
Chân lối cao trùng với tâm mặt mũi lòng (Tâm lòng là trọng tâm tam giác ABC)
Tất cả những góc tạo nên vì thế cạnh mặt mũi và mặt mũi lòng đều vì thế nhau
Tất cả những góc tạo nên vì thế những mặt mũi mặt và mặt mũi lòng đều vì thế nhau

Chú ý:

+ Tâm của tam giác đều là phó điểm 3 lối trung tuyến, cũng chính là lối cao, trung trực và phân giác vô.
+ Tâm của hình vuông vắn đó là phó điểm hai tuyến đường chéo cánh.

b. Diện tích hình chóp đều

- Diện tích xung xung quanh của hình chóp đều tiếp tục bằng tích của nửa chu vi đáy với trung đoạn:

S_xq = p.d
(với p là nửa chu vi lòng, d là trung đoạn)

- Diện tích toàn phần của hình chóp tiếp tục vì thế tổng của diện tích S xung xung quanh và diện tích S mặt mũi lòng. Ta đem công thức sau đây:

S_tp = S_xq + S
(với S là không gian đáy)

Ví dụ :

Cho một hình chóp tam giác đều đem chiều lâu năm cạnh lòng là 4cm và trung đoạn của hình chóp tam giác đều là 2cm. Hãy mò mẫm diện tích S xung xung quanh của hình chóp tam giác đều đó?

Lời giải:

Đầu tiên, theo dõi công thức tính diện tích S xung xung quanh của hình chóp tam giác đều một vừa hai phải nêu bên trên, tao cần thiết xác lập được nửa chu vi của lòng hình chóp tam giác đều là từng nào.

Vì là hình chóp tam giác đều nên lòng của hình chóp là một trong tam giác đều. Từ bại liệt, tao vận dụng công thức tính nửa chu vi hình tam giác đều.

Nửa chu vi lòng của hình chóp tam giác đều là:

p = (3 x 4) ÷ 2 = 6 (cm)

→ Diện tích xung xung quanh của hình chóp tam giác đều là:

S xung xung quanh = p * d

=> S xung xung quanh = 6 x 2 = 12 (cm²)

→ Kết luận: diện tích S xung xung quanh của hình chóp tam giác đều là 12 cm² .

c. Thể tích hình chóp tam giác đều S.ABC là ${V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SO$ ${V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SO$

Trong đó: ${S_{ABC}}$ ${S_{ABC}}$ là diện tích S lòng tam giác đều ABC

SO là lối cao kẻ kể từ S xuống tâm O mặt mũi lòng ABC

Ví dụ 1: Cho hình chóp tam giác đều S_ABC cạnh lòng vì thế a và cạnh mặt mũi vì thế 2a. Chứng minh rằng chân lối cao kẻ kể từ S của hình chóp là tâm của tam giác đều ABC. Tính thể tích chóp đều S_ABC.

Hướng dẫn trả lời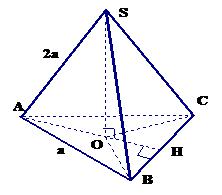
Hình chóp đều: Hình chóp đều tam giác, hình chóp đều tứ giác

Giải: Dựng SO⊥ ΔABC, Ta đem SA = SB = SC suy rời khỏi OA = OB = OC

Vậy O là tâm của tam giác đều ABC.

Ta có: AO = $\frac{2}{3}AH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}$ $\frac{2}{3}AH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}$

Tam giác ABC đều nên tam giác SAO vuông, vận dụng Pi - tao - go tao có: $S{O^2} - O{A^2} = \frac{{11{a^2}}}{3}$ $S{O^2} - O{A^2} = \frac{{11{a^2}}}{3}$

$\Rightarrow SO = \frac{{a\sqrt {11} }}{{\sqrt 3 }}$ $\Rightarrow SO = \frac{{a\sqrt {11} }}{{\sqrt 3 }}$

$\Rightarrow V = \frac{1}{3}.{S_{ABC}}.SO = \frac{{{a^3}\sqrt {11} }}{{12}}$ $\Rightarrow V = \frac{1}{3}.{S_{ABC}}.SO = \frac{{{a^3}\sqrt {11} }}{{12}}$

d. Cách vẽ hình chóp tam giác đều :

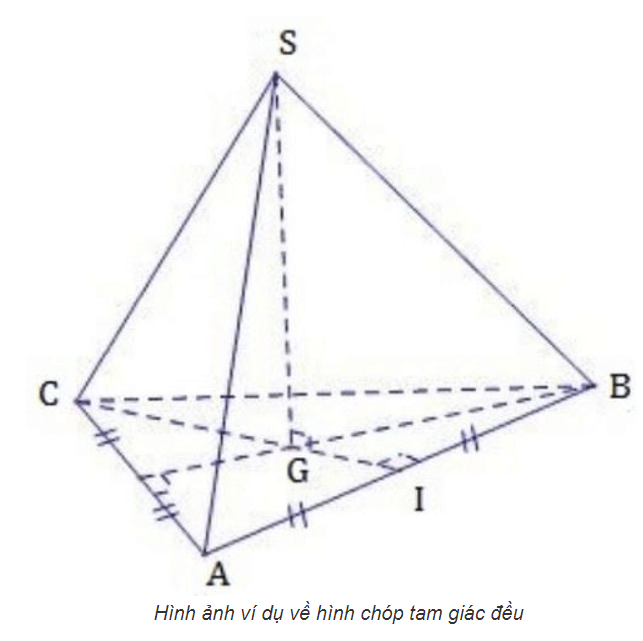
Muốn giải một câu hỏi hình bất kì này bại liệt thì việc thứ nhất tất cả chúng ta cần thiết thực hiện một cơ hội thiệt đúng mực và kỹ lưỡng đó là vẽ đúng mực hình tuy nhiên đề bài xích thể hiện.

Và những câu hỏi về hình chóp tam giác đều cũng vậy, không chỉ có thế, vẽ hình cũng trực thuộc hạng mục được xem điểm Lúc lên đường đua chính vì thế chúng ta cần thiết chú ý yếu tố này nhằm tách bị rơi rụng điểm.

Muốn vẽ được hình chóp tam giác đều đúng mực và dễ dàng và đơn giản thì chúng ta cần thiết triển khai 3 bước theo dõi trật tự sau đây:

Bước 1: vẽ một hình tam giác đều ABC (nhưng ko cần thiết nhất thiết tía cạnh nên đều nhau, rất có thể vẽ một hình tam giác thông thường vì thế vô hình học tập không khí là hình 3 chiều vì vậy coi theo dõi những góc nhìn không giống nhau thì phỏng lâu năm những cạnh sẽ sở hữu sự thay cho đổi),
Bước 2: Lần lược, vẽ 2 đường trung tuyến AI và CF tách nhau bên trên điểm O, và điểm O này cũng đó là chân lối cao của đỉnh hình chóp trùng với tâm lòng (tâm của tam giác đều ABC),
Bước 3: Từ O, tao dựng 1 đường thẳng liền mạch đứng, kể từ bại liệt tao dành được đỉnh S của hình chóp. Cuối nằm trong, theo lần lượt nối đỉnh S của hình chóp với 3 đỉnh A, B, C của lòng hình chóp (tức tam giác đều ABC).

→ Ta hoàn thiện hình vẽ và chiếm được một hình chóp tam giác đều S.ABC, với SH là lối cao và SA = SB = SC.

3. Hình chóp tứ giác đều

- Hình chóp tứ giác đều là hình chóp đem lòng là hình vuông vắn và lối cao của chóp trải qua tâm lòng (giao của 2 lối chéo cánh hình vuông).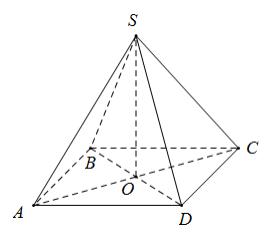 Hình chóp đều: Hình chóp đều tam giác, hình chóp đều tứ giác

a. Tính hóa học hình chóp tứ giác đều:

Đáy là hình vuông
Tất cả những cạnh mặt mũi vì thế nhau
Tất cả những mặt mũi mặt là những tam giác thăng bằng nhau
Chân lối cao trùng với tâm mặt mũi đáy
Tất cả những góc tạo nên vì thế cạnh mặt mũi và mặt mũi lòng vì thế nhau
Tất cả những góc tạo nên vì thế những mặt mũi mặt và mặt mũi lòng đều vì thế nhau

b. Diện tích hình chóp tứ giác đều

- Diện tích xung xung quanh của hình chóp đều tiếp tục bằng tích của nửa chu vi đáy với trung đoạn:

S_xq = p.d
(với p là nửa chu vi lòng, d là trung đoạn)

- Diện tích toàn phần của hình chóp tiếp tục vì thế tổng của diện tích S xung xung quanh và diện tích S mặt mũi lòng. Ta đem công thức sau đây:

S_tp = S_xq + S
(với S là không gian đáy)

c. Thể tích hình chóp tứ giác SABCD là: $V = \frac{1}{3}.{S_{ABCD}}.SO$ $V = \frac{1}{3}.{S_{ABCD}}.SO$

Trong đó: SABCD là diện tích S hình vuông vắn ABCD

SO là lối cao kẻ kể từ O xuống tâm lòng ABCD

Ví dụ 2: Cho khối chóp tứ giác S_ABCD đem toàn bộ những cạnh có tính lâu năm vì thế a. Chứng minh rằng S_ABCD là chóp tứ giác đều. Tính thể tích khối chóp S_ABCD.

Hướng dẫn trả lời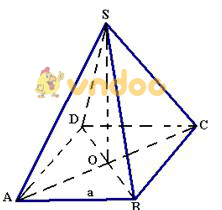
/data/image/2018/09/11/hinh-chop-deu-hinh-chop-deu-tam-giac-hinh-chop-deu-tu-giac-3.jpg

Giải:

Dựng SO⊥(ABCD)

Ta đem SA = SB = SC = SD nên OA = OB = OC = OD

=> ABCD là hình thoi đem lối tròn xoe nước ngoài tiếp nên ABCD là hình vuông vắn.

Ta đem SA² + SB² = AB² + BC² = AC² nên ΔASC vuông bên trên S

$\Rightarrow SO = \frac{{a\sqrt 2 }}{2}$ $\Rightarrow SO = \frac{{a\sqrt 2 }}{2}$

$\Rightarrow V = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{h^2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{6}$ $\Rightarrow V = \frac{1}{3}.{S_{ABCD}}.SO = \frac{1}{3}.{h^2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{6}$

4. Phân biết hình chóp tam giác đều và hình chóp tứ giác đều:

- Hình chóp tam giác đều theo dõi đình tức là hình chóp đều sở hữu lòng là tam giác (mặt mặt mũi là tam giác cân nặng, ko đều).
- Hình chóp tứ giác đều theo dõi khái niệm là hình chóp đều sở hữu lòng là tứ giác (lúc này lòng là hình vuông vắn, mặt mũi mặt là tam giác cân).

5. Bài tập luyện trắc nghiệm hình chóp tam giác đều và hình chóp tứ giác đều

Câu 1: Thể tích của hình chóp tứ giác đều sở hữu độ cao là 9cm, cạnh lòng là 5cm là :

A.75 cm³ .

B. 225 cm³ .

C. 180 cm³ .

D. 60 cm³ .

Câu 1: Cho hình chóp S.ABCD đem lòng ABCD là hình vuông vắn cạnh vì thế 3cm, độ cao của hình chóp là h = 2cm. Thể tích của hình chóp đang được cho rằng :

A. 6 cm³ .

B. 18 cm³ .

C. 12 cm³ .

D. 9 cm³ .

Câu 2: Cho hình chóp tam giác đều sở hữu phỏng lâu năm cạnh lòng là 5cm, phỏng lâu năm trung đoạn của hình chóp là 6cm. Diện tích xung xung quanh của hình chóp tam giác đều này là :

A. 40 cm² .

B. 36 cm² .

C. 45 cm² .

D. 50 cm² .

Câu 3. Diện tích xung xung quanh của hình chóp đều bằng

A.Tích nửa chu vi lòng và độ cao của hình chóp.

B.Tích nửa chu vi lòng và trung đoạn .

C.Tích chu vi lòng và trung đoạn .

D.Tổng chu vi lòng và trung đoạn .

5. Hình chóp tam giác đều và hình chóp tứ giác đều sách mới

Bài 1: Hình chóp tam giác đều - Hình chóp tứ giác đều CTST
Bài 1: Hình chóp tam giác đều Cánh diều
Bài 2: Hình chóp tứ giác đều Cánh diều