Trong nội dung bài viết này hãy nằm trong mò mẫm hiểu đàng tầm của tam giác là gì và một vài ba những tấp tểnh lý và bài bác luyện nhé
Chắc hẳn chúng ta học viên thân quen gì với đường tầm của tam giác nhập toán học tập, tuy nhiên ko nên người nào cũng làm rõ khái niệm gần giống công thức của chính nó, nằm trong mò mẫm hiểu ngay lập tức về đàng tầm của tam giác nhập nội dung bài viết này nhé
1. Định nghĩa đàng tầm tam giác
Trong toán học tập, đường tầm của tam giác được khái niệm là đoạn trực tiếp nối nhì trung điểm ngẫu nhiên nhập một tam giác, phụ thân cạnh của tam giác sẽ khởi tạo rời khỏi phụ thân đàng tầm và đàng tầm của tam giác sẽ khởi tạo rời khỏi những cặp cạnh tỉ lệ thành phần cùng nhau và tuy nhiên song với cạnh còn sót lại.
Trong tình huống đặc biệt quan trọng, nếu như trong trường hợp là tam giác đặc biệt quan trọng như tam giác đều hoặc tam giác cân nặng, đàng tầm của những tam giác này rất có thể vị nửa cạnh loại ba
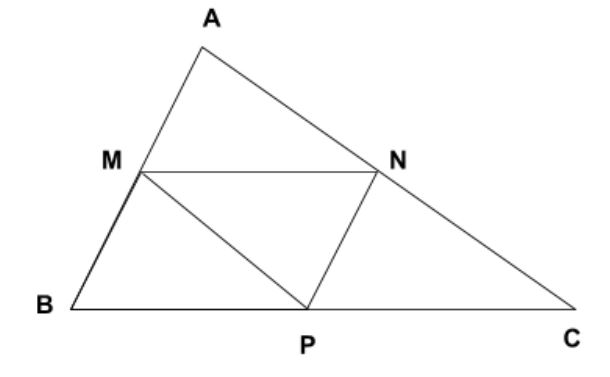
MN là đàng tầm của tam giác ABC
2. Định lý về đàng tầm nhập tam giác
Trong một vài ba dạng bài bác luyện, cần thiết làm rõ về những tấp tểnh lý của đường tầm nhập tam giác mới mẻ rất có thể thực hiện đích đòi hỏi của đề bài bác. Đường tầm của tam giác đem 2 tấp tểnh lý chính
Định lý 1
Trong một tam giác, nếu như một đường thẳng liền mạch trải qua một cạnh của tam giác và tuy nhiên song với cạnh loại nhì thì đường thẳng liền mạch ê trải qua trung điểm của cạnh loại ba
Dạng bài bác thông thường bắt gặp ở tấp tểnh lý này là dạng bài bác tương quan cho tới cạnh và góc, bao hàm phương pháp tính và chứng tỏ những hệ thức về cạnh và góc
Định lý 2
Đường tầm của tam giác vị ½ cạnh loại 3 và tuy nhiên song với cạnh ấy. Dạng toán thông thường được vận dụng là chứng tỏ một đường thẳng liền mạch là đàng tầm của một tam giác
3. Tính hóa học của đàng tầm của tam giác
- Một đường thẳng liền mạch trải qua trung điểm của một cạnh của tam giác và tuy nhiên song với 1 cạnh loại 3 thì tiếp tục trải qua trung điểm của cạnh thứ hai (cạnh còn lại)
- Đường tầm của tam giác luôn luôn tuy nhiên song với cạnh loại phụ thân và vị ½ chừng lâu năm của cạnh đó
Trong những dạng bài bác luyện tương quan đa số người học tập đều nên áp dụng những đặc thù đàng tầm nhằm chứng tỏ những đẳng thức và đòi hỏi đề ra
Tính hóa học đàng tầm của tam giác vuông
Tam giác vuông là tam giác đem 2 cạnh tạo ra một góc 90 chừng, Lúc nối 2 trung điểm của 2 cạnh góc vuông tao sẽ tiến hành một đàng tầm tuy nhiên song với cạnh còn sót lại, còn Lúc nối trung điểm của một cạnh góc vuông và 1 cạnh thông thường thì đàng tầm tiếp tục vuông góc với 1 cạnh góc vuông
VD:

Ví dụ về đàng tầm nhập tam giác vuông
Trong tam giác vuông MNP tao đem OQ là đàng tầm của tam giác và OQ tuy nhiên song và vị 1/2 cạnh MN. điều đặc biệt đấy là tình huống tam giác vuông nên OQ tiếp tục vuông góc với MP
Cách chứng tỏ đàng tầm của tam giác vuông
Để chứng tỏ 1 đường thẳng liền mạch là đàng tầm của tam giác vuông thì trước không còn đường thẳng liền mạch ê nên tuy nhiên song với 1 trong phụ thân cạnh của tam giác
Tiếp bám theo thì đường thẳng liền mạch nên đáp ứng nhu cầu đòi hỏi là vuông góc với một nhập 2 cạnh góc vuông của tam giác vuông
Đặc biệt, đàng tầm của tam giác vuông hoặc được contact và áp dụng trong số dạng bài bác của hình thang vuông, bạn phải nắm vững về phần lý thuyết này nhằm học tập dĩ nhiên những phần sau.
4. Các dạng toán phổ cập về đàng tầm của tam giác
Dạng 1: Dạng tương quan cho tới cạnh và góc, bao hàm những dạng như tính chừng lâu năm cạnh, số chừng của góc hoặc chứng tỏ những hệ thức liên quan
Để rất có thể xử lý dạng toán này, cách thức được vận dụng đa số là phụ thuộc đặc thù đàng tầm của tam giác kết phù hợp với những kỹ năng về góc và cạnh không giống. Cụ thể là tấp tểnh lý 1 và tấp tểnh lý 2 như tiếp tục nêu ở trên
Dạng 2: Là dạng chứng tỏ một đường thẳng liền mạch bất kì là đàng tầm của tam giác.
Để rất có thể thực hiện được dạng bài bác luyện này, bạn phải hiểu và vận dụng khái niệm đàng tầm của tam giác. Từ kỹ năng đàng tầm là đoạn trực tiếp nối trung điểm nhì cạnh của tam giác lại cùng nhau tao tiếp tục chứng tỏ được đường thẳng liền mạch này đó là đàng tầm của tam giác
5. Một số bài bác luyện kiểu mẫu về đàng tầm nhập tam giác
Bài luyện 1:
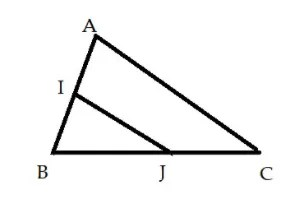
Hình minh họa bài bác luyện 1
Xét tam giác ABC có:
- I là trung điểm của AB
- J là trung điểm của BC
Theo tấp tểnh lý đàng tầm của tam giác tao suy rời khỏi được IJ là đàng tầm tam giác ABC
Bài luyện 2: Cho tam giác MNP, những đàng trung tuyến NA và PB rời nhau ở C. Gọi D, E bám theo trật tự là trung điểm của NA, BP. Chứng minh rằng BA//DE, BA= DE.
* Trong MNP, tao có:
B là trung điểm của MN (giả thiết)
A là trung điểm của MP (giả thiết)
Nên AB là đàng tầm của MNP
Theo đặc thù đàng tầm của tam giác
AB//DE và AB = NP/2 (1)
* Trong NPC, tao có:
D là trung điểm của NC (gt)
E là trung điểm của PC (gt)
Nên DE là đàng tầm của NPC
Lại kể từ đặc thù đàng tầm tam giác, suy ra:
DE // NP và DE = NP/2 (2)
Từ (l) và (2) suy ra: AB // DE, AB = DE
Một số bài bác luyện tập thêm
Bài 1: Cho tam giác ABC, đem AM là trung tuyến ứng với BC. Trên cạnh AB lấy điểm D và E sao mang đến AD = DE = EB. Đoạn trực tiếp CD rời AM bên trên điểm I. Chứng minh rằng
a) EM // DC
b) I là trung điểm AM
c) DC = 4DI
Bài 2: Cho tam giác ABC cân nặng bên trên A, đem M là trung điểm của BC. Kẻ tia Mx tuy nhiên song với AC rời AB bên trên E và tia My tuy nhiên song với AB rời AC bên trên F. Chứng minh:
a) EF là đàng tầm của tam giác ABC;
b) AM là đàng trung trực của EF.
Bài 2: Cho hình thang ABCD vuông bên trên A và D. Gọi E, F thứu tự là trung điểm của AD và BC. Chứng minh
a) AFD cân nặng bên trên F
b) Tam giác BAF =Tam giác CDF
Bài 3: Cho tam giác ABC đem AM là trung tuyến ứng với cạnh BC. Trên cạnh AC lấy điểm D sao mang đến AD = ½ DC. Kẻ Mx tuy nhiên song tuy nhiên với BD và rời AC bên trên E. Đoạn BD rời AM bên trên I. Chứng minh rằng:
a) AD = DE = EC;
b) SAIB = SIBM ;
c) SABC = SIBC .
Bài 4: Cho tam giác ABC vuông bên trên A, đàng cao AH. Từ H kẻ Hx vuông góc với AB bên trên P.., Hy vuông góc với AC bên trên Q. Trên những tia Hx, Hy thứu tự lấy những điểm D và E sao mang đến PH = PD; QH = QE. Chứng minh:
a) A là trung điểm của DE
b) PQ = ½ DE
c) PQ = AH
Kết luận: Bài ghi chép bên trên là toàn cỗ những kỹ năng cần thiết tương quan cho tới đường tầm của tam giác, chúng ta cần thiết nắm vững những kỹ năng như tấp tểnh lý và đặc thù nhằm áp dụng nhập bài bác luyện. Để hiểu thêm nhiều hình thức bài bác cũng như các vấn đề toán học tập hữu ích hãy nối tiếp bám theo dõi Cửa Hàng chúng tôi nhé.
