Định lý hàm cosin là 1 ấn định lý vô giải tích, về độ quý hiếm cosin của một góc ở trong vòng kể từ 0 cho tới π/2 luôn luôn nhỏ rộng lớn hoặc tự 1. Định lý này hỗ trợ một số lượng giới hạn bên trên cho tới độ quý hiếm của hàm cosin và được vận dụng rộng thoải mái trong số vấn đề tương quan cho tới tam giác và lượng giác. Vì vậy, định lý hàm cosin là 1 trong mỗi kỹ năng và kiến thức cần thiết vô trong cả quy trình học tập toán ở ngôi trường trung học tập phổ thông. Nhằm chung những em học viên đơn giản và dễ dàng ghi lưu giữ và vận dụng ấn định lý Cosin, VOH Giáo dục đào tạo đang được tổ hợp toàn bộ kỹ năng và kiến thức bao gồm ấn định lý, hệ trái khoáy và tính phần mềm của nới, chào những em tham ô khảo:
1. Định lý hàm cosin vô tam giác
Trong một tam giác, tớ tuyên bố ấn định lý hàm cosin như sau: Trong một tam giác, bình phương một cạnh tự tổng của nhị cạnh bại trừ cút nhị phiên tích của bọn chúng với cosin của góc xen thân thiết nhị cạnh bại.
Trong tam giác ABC, với AB = c, BC = a, AC = b tớ có:

Như vậy, vô một tam giác nếu như hiểu rằng nhị cạnh và góc xen thân thiết tớ tiếp tục tính được chừng nhiều năm của cạnh sót lại.
Chứng minh ấn định lý hàm số cosin
Để minh chứng ấn định lý này chúng ta cũng có thể vận dụng cách thức bên dưới đây:
Cho tam giác ABC với BC = a, AC = b, AB = c.
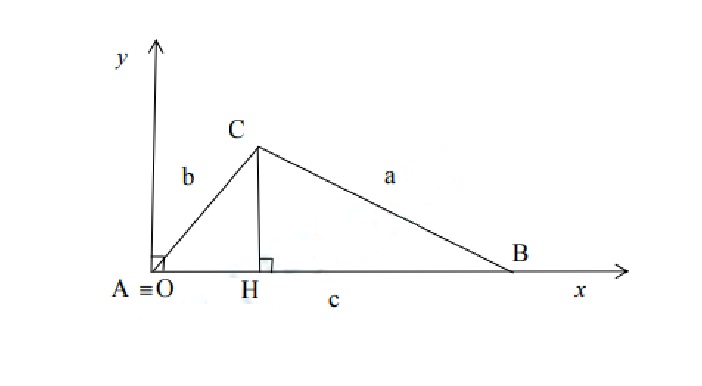

2. Hệ trái khoáy ấn định lý hàm cosin
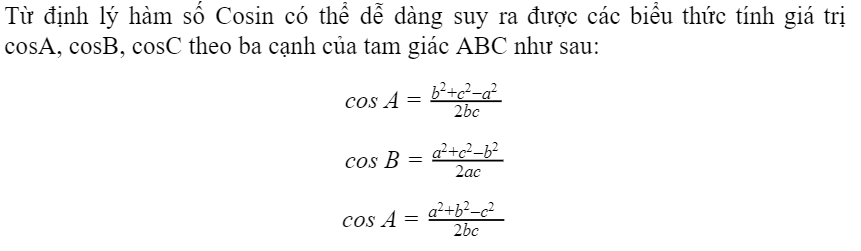
Như vậy hệ trái khoáy của định lý hàm cosin đã cho chúng ta thấy nếu như hiểu rằng chừng nhiều năm của 3 cạnh tớ tiếp tục tính được số đo của những góc. Hay hoàn toàn có thể hiểu đơn giản và giản dị rằng ấn định lý hàm số cosin sẽ hỗ trợ tớ tính được chừng nhiều năm của cạnh thì hệ trái khoáy của ấn định lý này sẽ hỗ trợ tất cả chúng ta tính được số đo của góc.
Bên cạnh bại, việc vận dụng ấn định lý hàm số Cosin hoàn toàn có thể giúp chúng ta tìm kiếm được chừng nhiều năm những đàng trung tuyến theo đuổi thân phụ cạnh của một tam giác. Cụ thể:
Trong tam giác ABC, với AB = c, BC = a, AC = b. Nếu bịa những đàng trung tuyến kẻ kể từ những đỉnh A, B, C theo thứ tự là , , thì :
3. Ứng dụng của ấn định lý hàm cosin
Định lý hàm cosin là 1 trong mỗi phần kỹ năng và kiến thức cơ bạn dạng, xuyên thấu vô công tác toán học tập phổ thông. Một số ví dụ về phần mềm của ấn định lí cosin vô giải toán những chúng ta cũng có thể tham ô khảo:

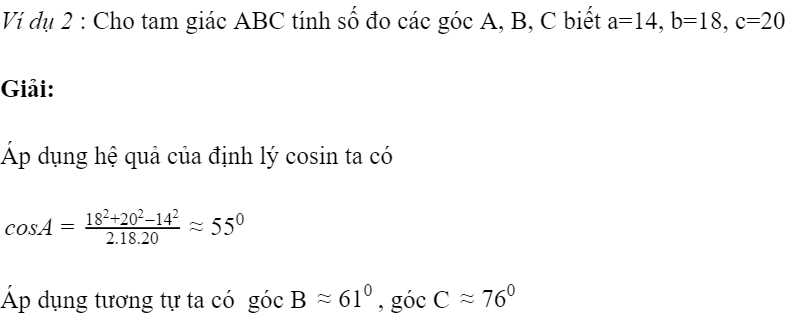
Ngoài đi ra, hoàn toàn có thể vận dụng ấn định lý hàm cosin nhằm tính tam giác vô thực thế. Trong thực tiễn có tương đối nhiều vấn đề đòi hỏi tính độ cao của một cây cao nào là bại hay 1 tòa ngôi nhà nào là này mà tớ ko thể trèo lên tới đỉnh của chính nó nhằm đo thẳng được. Chẳng hạn như ham muốn đo độ cao của tháp Eiffel tớ cũng ko thể trèo Tột Đỉnh của chính nó tuy nhiên kéo thước thừng nhằm đo thẳng được. Vậy nhằm đo độ cao của chính nó thì tớ tiếp tục vận dụng định lý hàm số cos vô việc giải tam giác nhằm tính độ cao theo đuổi đòi hỏi.
Những share về định lý hàm cosin kể từ VOH Giáo dục đào tạo vừa vặn hỗ trợ khao khát rằng hoàn toàn có thể chung những em học viên hiểu rộng lớn về phần kỹ năng và kiến thức này. Từ bại hoàn toàn có thể đơn giản và dễ dàng vận dụng giải toán.
