Hình thoi là tứ giác sở hữu tứ cạnh đều nhau, là tứ giác sở hữu hai tuyến phố chéo cánh vuông góc cùng nhau bên trên trung điểm của từng lối là hình thoi, là hình bình hành sở hữu nhì cạnh kề bởi nhau… Mé cạnh hình vuông vắn, chữ nhật, tam giác… thì hình thoi là 1 trong trong mỗi hình cần thiết nhập toán học tập và cuộc sống đời thường.
Bên cạnh công thức tính chu vi, diện tích S hình thoi thì phương pháp tính lối chéo cánh hình thoi - lối nối những đỉnh đối lập của hình thoi lại cùng nhau, cũng tương đối cần thiết.
Bài viết lách tiếp sau đây tiếp tục khiến cho bạn dò thám hiểu về kiểu cách tính lối chéo cánh hình thoi tất nhiên những ví dụ rõ ràng, mời mọc xem thêm.
Đường chéo cánh của hình thoi

- Đường chéo cánh của hình thoi là lối nối nhì đỉnh đối lập của hình thoi.
- Hình thoi sở hữu hai tuyến phố chéo cánh, và bọn chúng rời nhau bên trên trung điểm của hình thoi.
- Đường chéo cánh phân chia hình thoi trở nên nhì tam giác đều với những cạnh đều nhau.
Tính hóa học hai tuyến phố chéo cánh hình thoi
Hai lối chéo cánh nhập hình thoi sở hữu những đặc điểm sau:
- Hai lối chéo cánh bởi nhau: Hai lối chéo cánh của hình thoi có tính nhiều năm đều nhau.
- Góc thân thuộc hai tuyến phố chéo cánh là góc vuông: Hai lối chéo cánh của hình thoi rời nhau bên trên trung điểm của hình thoi và tạo ra trở nên một góc vuông.
- Đường chéo cánh là trục đối xứng của hình thoi: Mỗi lối chéo cánh của hình thoi là trục đối xứng của hình thoi, phân chia hình thoi trở nên nhì nửa đối xứng.
- Đường chéo cánh là lối chéo cánh của nhì tam giác đều: Mỗi lối chéo cánh của hình thoi là lối chéo cánh của nhì tam giác đều, được tạo ra trở nên bởi những cạnh đều nhau.
- Tích của phỏng nhiều năm hai tuyến phố chéo cánh bởi tích của phỏng nhiều năm nhì cạnh góc vuông của hình thoi: Tích của phỏng nhiều năm hai tuyến phố chéo cánh của hình thoi bởi tích của phỏng nhiều năm nhì cạnh góc vuông của hình thoi. Tức là, nếu như tất cả chúng ta ký hiệu lối chéo cánh là d, cạnh góc vuông là a và b, tớ sở hữu d² = a² + b².
Những đặc điểm này là những đặc điểm đặc thù của hình thoi và được dùng trong tương đối nhiều câu hỏi hình học tập tương quan cho tới hình thoi.
Công thức tính lối chéo cánh hình thoi
Mời chúng ta cũng xét ví dụ tiếp sau đây nhằm kể từ ê thể hiện được công thức tính đường chéo hình thoi.
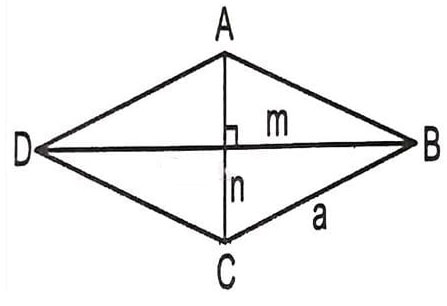
Giả sử tớ cần thiết tính phỏng nhiều năm lối chéo cánh hình thoi ABCD sở hữu cạnh a và một góc ABC = 60 phỏng -> công thức tính đường chéo hình thoi nhập tình huống này như vậy nào?
Lời giải:
Vì ABCD là hình thoi nên những cạnh đều bởi a.
Xét tam giác ABC có: AB = BC = a
Lại có: ABC = 60 phỏng => Tam giác ABC là tam giác đều cạnh a.
=> AB = AC = BC = a
=> Độ nhiều năm lối chéo cánh hình thoi đó là AC = BD = a.
Cách giải bên trên là 1 trong trong mỗi công thức tính đường chéo hình thoi giản dị và đơn giản và dễ nắm bắt nhất.
Công thức tính lối chéo cánh hình thoi lúc biết diện tích S và lối chéo cánh còn lại
Từ công thức tính diện tích S hình thoi:
S = (a x b) : 2
Ta sở hữu công thức phỏng nhiều năm lối chéo cánh như sau :
a = S x 2 : b
hoặc
b = S x 2 : a
Trong đó:
- S là diện tích
- a và b là phỏng nhiều năm 2 lối chéo
Sử dụng những đặc điểm hình học tập của hình thoi nhằm tính phỏng nhiều năm lối chéo cánh nhưng mà ko cần dùng tấp tểnh lý Pythagoras. Cụ thể:
Đường chéo cánh của hình thoi là khoảng nằm trong của hai tuyến phố cao.
Đường chéo cánh = căn bậc nhì của (đường cao nhiều năm + lối cao ngắn)²
Đường chéo cánh của hình thoi là nửa chu vi của hình thoi.
Đường chéo cánh = 50% x chu vi hình thoi.
Bài toán về tính chất lối chéo cánh hình thoi
Bài toán 1: Cho một hình thoi sở hữu diện tích S là 360 centimet vuông, phỏng nhiều năm một lối chéo cánh là 24 centimet . Tính phỏng nhiều năm lối chéo cánh loại hai
Lời giải :
Theo công thức diện tích S hình thoi: a x b : 2
Ta sở hữu lối chéo cánh loại 2: 360 x 2 : 24 = 30cm
Đáp án: 30cm
Bài toán 2:
Một hình thoi sở hữu diện tích S 4dm , phỏng nhiều năm một lối chéo cánh là 3/5 dm. Tính phỏng nhiều năm lối chéo cánh loại nhì.Lời Giải :
Độ nhiều năm lối chéo cánh loại nhì là:
(4 x 2) : 3/5 =40/3 (dm)
Bài 3: Hai lối chéo cánh của hình thoi có tính nhiều năm là 160cm và 120 centimet. Tính độ cao của hình thoi, biết tỉ số thân thuộc độ cao và phỏng nhiều năm cạnh hình thoi là 24:25.
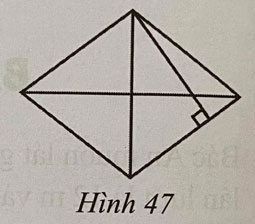
Lời giải:
Diện tích hình thoi là: 160.120:2 = 9 600 (cm2).
Vì tỉ số thân thuộc độ cao và phỏng nhiều năm cạnh hình thoi là 24:25 nên rất có thể coi độ cao hình thoi là 24a và cạnh hình thoi là 25a.
Khi ê tớ sở hữu diện tích S hình thoi là: 25a.24a = 9 600 a2 = 16 a = 4 centimet.
Chiều cao của hình thoi là: 24.4 = 96 (cm).
Vậy độ cao của hình thoi là 96cm.
Bài 4:
Cho hình thoi ABCD sở hữu cạnh bởi 12,5cm, lối cao bởi 6,72 centimet và AC nhỏ rộng lớn BD. Hỏi phỏng nhiều năm hai tuyến phố chéo cánh AC và BD theo lần lượt bởi bao nhiêu?
Giải:
Áp dụng công thức tính diện tích S hình thoi: S = h.a = 6,72 x 12, 5 = 84cm.
=> 50% AC x BD = 84 => 2AC.BD = 336
Gọi O là phú điểm của hai tuyến phố chéo cánh hình thoi.
Ta đã đạt được AOB là tam giác vuông bên trên O nên AB2 = OA2 + OB2
Trong ê, OA = 50% AC, OB = 50% BD
=> 12,52 = 1/4 (AC2 + BD2) <=> 625 = AC2 + BD2
AC2 + BD2 = 625 <=> AC2 + BD2+ 2AC.BD = 625 + 336 <=> (AC + BD)2 = 961 <=> AC + BD = 31 (1)
AC2 + BD2 = 625 <=> AC2 + BD2- AC.BD = 625 -336 <=> (BD - AC)2 = 289 <=> BD - AC = 17 (Theo đề bài xích BD > AC) (2)
Từ (1) và (2), tớ có:
BD = 24, AC = 7cm.
Bài 5:
Hình thoi ABCD sở hữu cạnh bởi 10 đơn vị chức năng. Tính phỏng nhiều năm lối chéo cánh của hình thoi.
Giải: Độ nhiều năm lối chéo cánh của hình thoi ABCD là:
Đường chéo cánh = căn bậc nhì của 2(10²) = căn bậc nhì của 200 = 14.14 đơn vị chức năng phỏng nhiều năm.
Vậy phỏng nhiều năm lối chéo cánh của hình thoi ABCD là 14.14 đơn vị chức năng phỏng nhiều năm.
Bài 6:
Hình thoi ABCD sở hữu lối chéo cánh bởi 12 đơn vị chức năng. Tính chu vi của hình thoi.
Giải: Vì hình thoi sở hữu tứ cạnh đều nhau, chu vi của chính nó được xem là tổng phỏng nhiều năm tứ cạnh, tức là:
Chu vi = 4 x phỏng nhiều năm cạnh = 4 x 6 = 24 đơn vị chức năng phỏng nhiều năm.
Vậy chu vi của hình thoi ABCD là 24 đơn vị chức năng phỏng nhiều năm.
